Transposing a Matrix using RISC-V Vector

Survey of basic techniques to transform matrix layouts using RVV

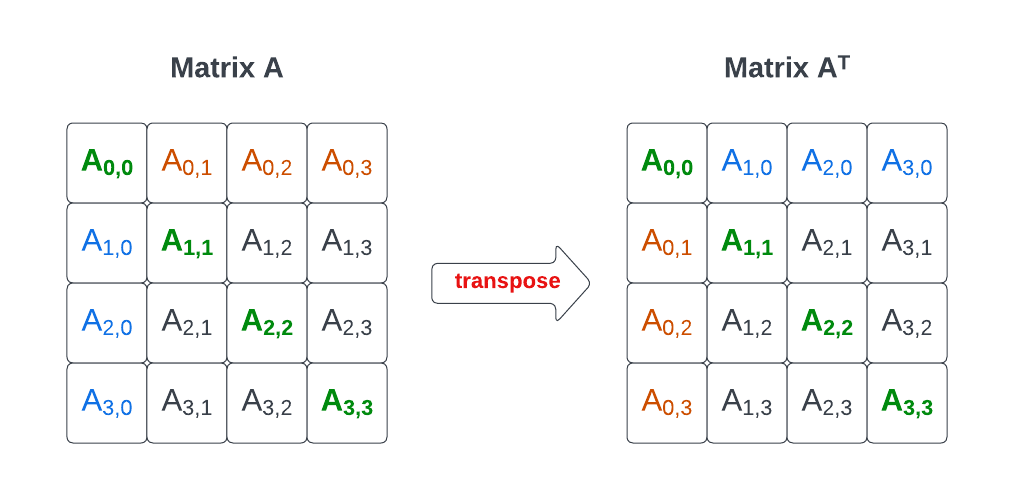
Transposing a square matrix¹ A is computing A^⊤ its symmetry with respect to its diagonal: the i-th row becomes the i-th column.

In Linear algebra, transposing a matrix is a standard operation which is useful in many linear algebra application. For example, if you want to multiply two matrices stored in row-major format (elements from the same row are stored contiguously in memory) it can be useful to first store the right hand side matrix in column-major layout before doing the multiplication. (Note that advanced matrix multiplication libraries such as BLIS use a much more advanced packing technique).

Matrix Data Layout

Let us first review the specification of what we want to implement and in particular how the input and output matrix should appear in memory (a.k.a. the data layout).

The following diagram represents how a dense 4x4 matrix A can be stored in memory, either as row major (top) or column major (bottom): in the row-major layout elements from a matrix row are stored contiguously in memory while elements from a column are spaced out by a constant byte stride equal to the number of elements in a row multiplied by the byte size of an element.

What is the relation between matrix layouts in memory and computing a matrix transpose ?

Transposing is simply going from one representation to the other. More specifically if you look at the row major memory layout of transposed matrix A^⊤, it is identical to the column major layout of the original matrix A.

Generic implementation

The base implementation we use, to generate golden value and benchmark against, is listed below:

void matrix_transpose(float *dst,
                      float *src,
                      size_t n) 
{
    size_t i, j;
    for (i = 0; i < n; ++i)
        for (j = 0; j < n; ++j) dst[i * n + j] = src[j * n + i];
};

We will use two baseline versions of the above code: the vanilla implementation and an implementation where n is fixed to the value 4 (allowing for dedicated optimization).

Note: although the baseline code does not explicitly invoke vector operation through intrinsics, any recent compiler will vectorize it on RVV and make use of some vector operations in the generated code. Therefore, this code should be seen as not explicitly vectorized (and not as non-vectorized at all).

Transposing Using Memory

4 x 4 matrix transpose using strided vector stores

Let’s review a first technique using RVV’s strided vector store operations, vsse*.v, to perform the matrix transpose. We will start with a matrix with static dimension: 4 by 4.

Strided memory operations read or write multiple elements in memory with a configurable uniform byte offset between each element (the stride). Vector strided memory operations were reviewed in our first post on vector memory operations:

RISC-V Vector extension in a nutshell (Part 5.1): vector loads and store

The code to perform matrix tranpose using vsse is rather straightfoward:

void matrix_transpose_intrinsics_4x4(float *dst, float *src) 
{
    unsigned i;
    for (i = 0; i < 4; ++i) {
        vfloat32m1_t row = __riscv_vle32_v_f32m1(src + 4 * i, 4);
        __riscv_vsse32(dst + i, sizeof(float) * 4,row, 4);
    }
}

The technique is simple: we use a unit-strided vle32 to load a matrix row from memory. Since the matrix has a row-major layout in memory, a row can be loaded with the unit-strided load operation for 32-bit elements:

        vfloat32m1_t row = __riscv_vle32_v_f32m1(src + 4 * i, 4);

The unit-strided source address corresponds to the start of the i-th row in memory: src + 4 * i. And since we need to load 4 elements, the last argument, vl (vector length) is set to 4.

Note: since RVV intrinsics distinguish between 32-bit floating-point and integer element type we use the function which returns a vector of floating-point elements, __riscv_vle32_v_f32m1, since we area loading data from a float*.

Then we use a strided store instruction, vsse32, to store each element from the source row 4 elements apart in the destination matrix, effectively storing them in different rows of the same column:

        __riscv_vsse32(dst + i, sizeof(float) * 4,row, 4);

The destination address is the start of the i-th column: dst + i. The byte stride is the size of a row (in bytes) and vl is still 4 (in our example of a square matrix, a column has as many element as the source row).

Note: in our code snippet, pointer arithmetic is performed on float*, so we add (or subtract) a number of elements to the base addresses. Strides are byte strides so we need to add the number of bytes in a row (not the number of elements).

Since rows contain 4 elements the vector strided store has the effect of storing the row as a column, thus realizing the transpose. We replicate this step 3 more times, once for each remaining pairs of input row / destination column while updating the source and destination addresses.

Note: This code snippet only works for implementation with VLEN >= 128 since we assume 4 floats fit in a single vector register group (vfloat32m1_t). For smaller VLENs one would have to extend the size of the intermediary register group used to store a row (e.g. vfloat32m4_t will work for VLEN>=32) or iterate over elements in a row (see next technique).

n x n matrix transpose using strided vector stores

Let us now generalize our 4 x 4 matrix transpose routine to work for any n x n square matrix. Our implementation will transpose each input row separately, using unit strided vector loads to read the row elements from memory and writing them back to memory as a column chunk using strided vector stores. The diagram below illustrates this new scheme. We load 4 elements from row i starting at column j and we store them back on row j, j+1, j+2, and j+3 of column i.

And now the code:

/** n x n matrix transpose using strided stores */
void matrix_transpose_intrinsics(float *dst, float *src, size_t n) 
{
    for (size_t row_id = 0; row_id < n; ++row_id) { // input row-index
        size_t avl = n;
        // source pointer to row_id-th row
        float* row_src = src + row_id * n;
        // destination pointer to row_id-th column
        float* row_dst = dst + row_id;
        while (avl > 0) {
            size_t vl = __riscv_vsetvl_e32m1(avl);
            vfloat32m1_t row = __riscv_vle32_v_f32m1(row_src, vl);
            __riscv_vsse32(row_dst, sizeof(float) * n, row, vl);
            // updating application vector length
            avl -= vl;
            // updating source and destination pointers
            row_src += vl;
            row_dst += vl * n;
        }
    }
}

nxn matrix transpose using strided vector loads

There is a symmetric technique using strided vector loads rather than stores. The vector memory instruction vlse32.v is used to load a chunk of a column into a vector register. This column chunk from the source matrix is a row chunk in the destination matrix and so we can use a unit-strided store vse32.v to write the row chunk to the destination buffer.

/** n x n matrix transpose using strided loads */
void matrix_transpose_intrinsics_loads(float *dst,
                                       float *src,
                                       size_t n) 
{
    for (size_t row_id = 0; row_id < n; ++row_id) { // input row-index
        size_t avl = n;
        float* col_src = src + row_id;
        float* row_dst = dst + row_id * n;
        while (avl > 0) {
            size_t vl = __riscv_vsetvl_e32m1(avl);
            // strided load to load a column into a vector register
            vfloat32m1_t row = __riscv_vlse32_v_f32m1(col_src, 
                                                      sizeof(float) * n,
                                                      vl);
            // unit-strided store to write back the column after 
            // tranpose (the row)
            __riscv_vse32(row_dst, row, vl);
            avl -= vl;
            col_src += vl * n;
            row_dst += vl;
        }
    }
};

4x4 matrix transpose using segmented vector stores

Matrix transpose can also be implemented using segmented memory operations. For a quick introduction on those instructions you can check out this post.

Here is an example of 4x4 matrix transpose using segmented loads:

void matrix_4x4_transpose_segmented_load(float* dst, float* src)
{
    vfloat32m1x4_t data = __riscv_vlseg4e32_v_f32m1x4(src, 4);
    vfloat32m1_t data0 = __riscv_vget_v_f32m1x4_f32m1(data, 0);
    vfloat32m1_t data1 = __riscv_vget_v_f32m1x4_f32m1(data, 1);
    vfloat32m1_t data2 = __riscv_vget_v_f32m1x4_f32m1(data, 2);
    vfloat32m1_t data3 = __riscv_vget_v_f32m1x4_f32m1(data, 3);
    vfloat32m4_t packedData = __riscv_vcreate_v_f32m1_f32m4(data0,
                                                            data1,
                                                            data2,
                                                            data3);
    __riscv_vse32_v_f32m4(dst, packedData, 16);
}

The code is very verbose because RVV intrinsics use a specific type format for segmented memory operations:

v<elt type>m<field group size>x<num fields>_t

So we need to reinterpret the vfloat32m1x4_t as a vfloat32m4_t. The generated assembly is much more concise than the C source code (compiler explorer):

        vsetivli      zero, 4, e32, m1, ta, ma
        vlseg4e32.v   v8, (a1)
        vsetivli      zero, 16, e32, m4, ta, ma
        vse32.v       v8, (a0)

This implementation relies on the fact that a 4x4 matrix can be seen as a vector of 4-field structures, where each structure represents a row in memory. The segmented vector load transposes the array of structures into a structure of arrays when loading the value into vector registers and each vector register is populated with the same index fields, that is the source matrix column.

A similar implementation can be built using a vsseg4e32.v vector segmented store:

void matrix_4x4_transpose_segmented_store(float* dst, float* src)
{
    // reading full 4x4 input matrix in row-major layout
    vfloat32m4_t data = __riscv_vle32_v_f32m4(src, 16);
    // extracting independent vector registers (rows)
    vfloat32m1_t data0 = __riscv_vget_v_f32m4_f32m1(data, 0);
    vfloat32m1_t data1 = __riscv_vget_v_f32m4_f32m1(data, 1);
    vfloat32m1_t data2 = __riscv_vget_v_f32m4_f32m1(data, 2);
    vfloat32m1_t data3 = __riscv_vget_v_f32m4_f32m1(data, 3);
    // building input for segmented store
    vfloat32m1x4_t packedData = __riscv_vcreate_v_f32m1x4(data0,
                                                          data1,
                                                          data2,
                                                          data3);
    // transposing using segmented store 
    __riscv_vsseg4e32_v_f32m1x4(dst, packedData, 4);
}

This time we do not need to unpack a segmented vector type, but we need to pack one.

In-register Method

We have seen multiple techniques to transpose a matrix using various RVV memory operations. It is also possible to implement matrix transpose using only register-to-register vector instructions. This can be useful if the matrix is already stored in a vector register group and if you want to avoid a round trip to memory. It can also be interesting if the target RVV implementation exhibits poor performance for strided or segmented memory accesses.

4x4 in-register transpose using vrgather(ei16)

The first in-register technique uses a vrgather(ei16).vv instruction. This instruction was presented in this post:

RISC-V Vector Extension in a Nutshell (Part 4): permute operations

We built a static vector of indices. This static vector encodes the transpose as a permutation: the i-th element in array offsetIndex contains the index of the source element which must be moved to the i-th destination element. We modified the transpose function API to accept a register group operand and to return result in a register group, that way it can be used for in-register transpose. The code is:

const uint16_t offsetIndex[] = {
    0, 4, 8, 12,
    1, 5, 9, 13,
    2, 6, 10, 14,
    3, 7, 11, 15
};

vfloat32m4_t matrix_4x4_transpose_vrgather(vfloat32m4_t src) {
    // loading array of indices
    vuint16m2_t indices = __riscv_vle16_v_u16m2(offsetIndex, 16);
    // performing transpose with in-register permutation
    return __riscv_vrgatherei16_vv_f32m4(src, indices, 16);
}

Note: Using vrgatherei16.vv rather than vrgather.vv allows to reduce the size of the index array and the amount of index data that needs to be moved around for element size greater than 16-bit.

The generated assembly is:

matrix_4x4_transpose_vrgather:          # @matrix_4x4_transpose_vrgather
.Lpcrel_hi0:
        auipc   a0, %pcrel_hi(offsetIndex)
        addi    a0, a0, %pcrel_lo(.Lpcrel_hi0)
        vsetivli        zero, 16, e32, m4, ta, ma
        vle16.v v16, (a0)
        vrgatherei16.vv v12, v8, v16
        vmv.v.v v8, v12
        ret

Note: the final vmv.v.v v8, v12 before the ret is necessary because a vrgather* destination group vd cannot overlap with any source group, vs2 or vs1, so vrgatherei16.vv v8, v8, v16 is not a legal instruction.

Note: the first two instructions materialize the index table address (which is built from a PC relative address on our case). They can change depending on how the static index array is declared and how it is positioned in memory by the compiler.

4x4 in-register transpose using masked vslides

Although performing a transpose using a vrgather instruction produces very compact code, it may not be the best solution. vrgather* are complex instructions which are not always fast, especially when working on large register groups.

To circumvent this limitation, we study another in-register transpose implementation based on masked vslide* instructions. This method is built from the following steps:

• Step (a): build 1x2 transposed segments packed into 1x4 vectors of 2 segments.

• Step (b): position the 1x2 segments built in step (a) in their correct position in the final rows.

For the step (a) we rely on vslideup.vi and vslidedown.vi with mask as illustrated below:

For step (b) we rely on the same instruction but we only need tail undisturbed behavior (and the standard vslideup behavior which does not modify the vector head):

Finally we can built the code to perform both steps:

vfloat32m4_t matrix_4x4_transpose_vslide(vfloat32m4_t src) {
    vfloat32m1_t inMat0 = __riscv_vget_v_f32m4_f32m1(src, 0);
    vfloat32m1_t inMat1 = __riscv_vget_v_f32m4_f32m1(src, 1);
    vfloat32m1_t inMat2 = __riscv_vget_v_f32m4_f32m1(src, 2);
    vfloat32m1_t inMat3 = __riscv_vget_v_f32m4_f32m1(src, 3);

    vuint32m1_t oddMask_u32 = __riscv_vmv_v_x_u32m1(0xaaaa, 1);
    vuint32m1_t evenMask_u32 = __riscv_vmv_v_x_u32m1(0x5555, 1);

    vbool32_t oddMask = __riscv_vreinterpret_v_u32m1_b32(oddMask_u32);
    // vl=4 in the following
    // should be mapped to vslideup.vi
    vfloat32m1_t transMat0 = __riscv_vslideup_vx_f32m1_tumu(oddMask,
                                                            inMat0,
                                                            inMat1,
                                                            1, 4);
    vfloat32m1_t transMat2 = __riscv_vslideup_vx_f32m1_tumu(oddMask,
                                                            inMat2,
                                                            inMat3,
                                                             1, 4);
   
    vbool32_t evenMask = __riscv_vreinterpret_v_u32m1_b32(evenMask_u32);
    // should be mapped to vslidedown.vi
    vfloat32m1_t transMat1 = __riscv_vslidedown_vx_f32m1_tumu(evenMask,
                                                              inMat1,
                                                              inMat0,
                                                              1, 4);
    vfloat32m1_t transMat3 = __riscv_vslidedown_vx_f32m1_tumu(evenMask,
                                                              inMat3,
                                                              inMat2,
                                                              1, 4);

    // should be mapped to vslideup.vi
    vfloat32m1_t outMat0 = __riscv_vslideup_vx_f32m1_tu(transMat0,
                                                        transMat2,
                                                        2, 4);
    vfloat32m1_t outMat1 = __riscv_vslideup_vx_f32m1_tu(transMat1,
                                                        transMat3,
                                                        2, 4);

    // vl=2 in the following
    // should be mapped to vslidedown.vi
    vfloat32m1_t outMat2 = __riscv_vslidedown_vx_f32m1_tu(transMat2,
                                                          transMat0,
                                                          2, 2);
    vfloat32m1_t outMat3 = __riscv_vslidedown_vx_f32m1_tu(transMat3,
                                                          transMat1,
                                                          2, 2);

    return __riscv_vcreate_v_f32m1_f32m4(outMat0,
                                         outMat1,
                                         outMat2,
                                         outMat3);
}

Note: there is no intrinsics for vslideup.vi / vslidedown.vi but __riscv_vslideup_vx/__riscv_vslidedown_vx will generate the expected instructions when called with a constant operand.

Benchmark(eting)

The full source code for all the examples presented in this post can be found on github: https://github.com/nibrunie/rvv-examples/tree/main/src/matrix_transpose.

We build the matrix transpose functions using clang version 18.0.0-git-5cfc7b33, and building with the options -O2 -march=rv64gcv and we execute them using spike/riscv-isa-sim. We measure the number of retired instructions for each implementations, the results are listed below (logarithmic scale):

Note: The usual warning applies: the number of retired instructions is a good metric to evaluate the compactness of an implementation (it will loosely correlate with the dynamic code size) but it is not really a good measurement of the program actual performance.

As expected, implementations with strided loads or strided stores exhibit the same number of retired instructions: those implementation are totally symmetric. The same conclusion can be drown for segmented loads and stores.

The implementations which require the less instructions are the segmented memory variants (loads or stores) with 5 retired instructions each. The in-register variant based on vrgatherei16, is next, requiring only 6 instructions. The instruction count can differ slightly from what we would expect by looking at the assembly generated from the code snippets presented earlier in this post.

Comparison of methods on different matrix sizes

In this second set of benchmarks we measure the number of retired instructions for different implementations across multiple matrix sizes: 4x4, 16x16, 128x128, and 512x512. We add two new implementations to the one previously benchmarked: an implementation based on strided vector store using LMUL=4 intermediary register group (rather than the LMUL=1 used in the default implementation) and another using LMUL=8.

The results are presented below:

Several remarks can be made. A first remark is that if VLMAX exceeds n there is no benefit to using a larger LMUL: for n=4 all the strided vector store implementation exhibit the same performance whether LMUL=1, 4 or 8. This is also visible for n=16 between LMUL=4 and LMUL=8 vector strided implementations

A second remark is that vector strided based implementation with LMUL=1 are less efficient than the baseline implementation when the value of n increases. The baseline implementation prolog and epilog costs which was predominant for smaller n become less important for larger values and the loop average cost become predominant.

Conclusion

We have surveyed multiple techniques to implement matrix tranpose using memory round-trip or in-register data manipulation. Those basic techniques can certainly be improved and refined but their should give you an overview of how to implement such data layout transformation and be able to tune your implementation to your specific needs (matrix size static/dynamic, micro-architecture efficiency for one operation or the other, code size importance …).

Appendix: running the benchmarks

# Cloning rvv-examples repository
git clone https://github.com/nibrunie/rvv-examples.git

# Entering matrix transpose directory
cd rvv-examples/src/matrix_transpose/

# Building and running the benchmarks (assuming suitable environment)
# you can refer to the repository's README.md file for guidelines on
# how to build such an environment in a docker image
make sim_bench_matrix_transpose

References:

• BLIS: BLAS-like Library Instantiation Software Framework https://github.com/flame/blis

• Github repository for the examples presented in this post: https://github.com/nibrunie/rvv-examples/tree/main/src/matrix_transpose

1. Transpose is defined beyond square matrix but we will focus on square matrices only in this post.