Quick Note: swapping pairs with RVV

A touch of low level programming

In this (very) short post, we are going to dive into a couple of implementation techniques to swap pairs of elements using RISC-V Vector. This algorithm appeared in our NTT implementation at the start of the “reconstruction phase”: the very first stage combines the permuted vector with itself pairwise swapped.

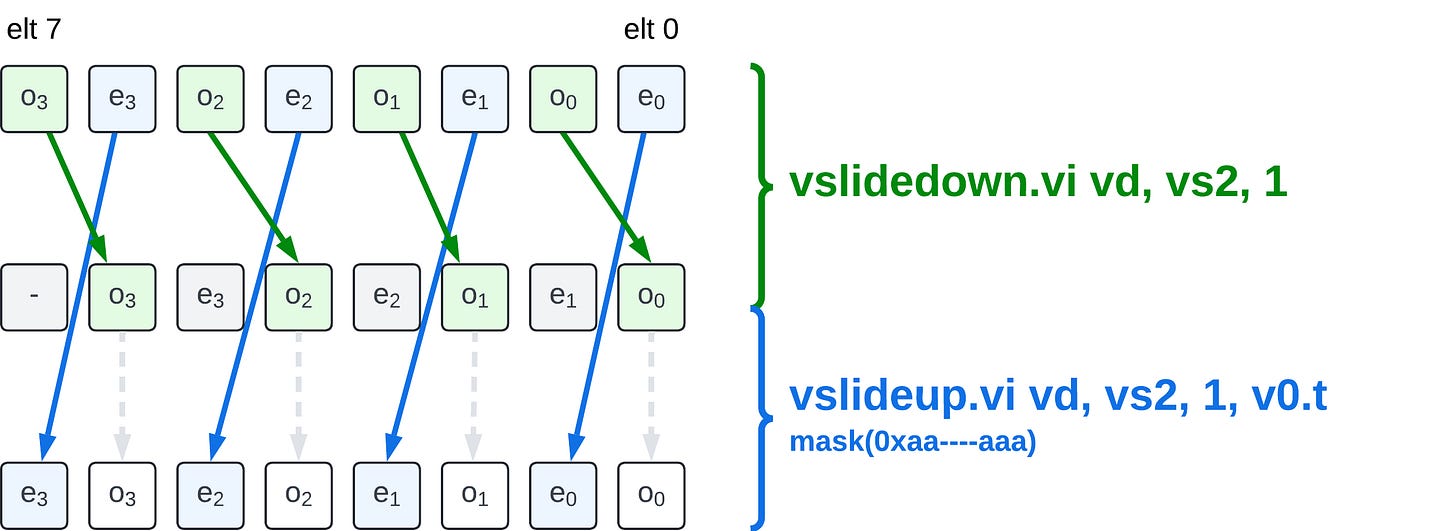
The function we want to implement is illustrated by the figure below (for an 8-element vector):

The vector is partitioned into consecutive 2-element pairs and the function consists in swapping the order of each pairs.

Using vslidedown and masked vslideup

This technique uses a pair of vslidedown.vi and masked vslideup.vi to perform the element swap. The vslidedown.vi is first executed to extract the odd elements from the input and position them in the even positions in the destination vector register group (this operation does not need to be masked, it also slides down the even elements, but those will be overwritten); then the masked vslideup.vi is executed to extract the even elements from the input and position them in the odd result positions. Both instructions target the same destination register group, and the vslideup.vi is masked, not to overwrite the work done by the vslidedown.vi.

We can look at the C-intrinsic implementation of this method (for a refresher on RVV intrinsics, you can checkout this post):

size_t vlmax = __riscv_vsetvlmax_e32m1();

// materializing required mask(s)
// broadcasting the byte value 0xaa to a whole vector
vint8m1_t mask_up_i8  = __riscv_vmv_v_x_i8m1(0xaa, vlmax);
// casting value to a vector mask type
vbool32   mask_up_b32 = __riscv_vreinterpret_v_i8m1_b32(mask_up_i8);

// performing odd/even pair swap on vl elements (vl / 2 pairs)
// vl is of type size_t
vint32m1_t vec_swapped_coeffs;
vec_swapped_coeffs = __riscv_vslidedown_vx_i32m1(vec_coeffs, 1, vl);
vec_swapped_coeffs = __riscv_vslideup_vx_i32m1_mu(mask_up_b32,
                                                  vec_swapped_coeffs,
                                                  vec_coeffs, 1, vl);

(source code in poly_mult_rvv.c#L233-L234, the code was modified for clarity, removing macros abstracting the LMUL values)

Note: the code above can be easily generalized to any LMUL. Only the LMUL used in the vslides need to be modified. The LMUL used when building does not need to differ from LMUL=1: a mask is at most VLEN-bit wide and has an EMUL <= 1.

Note: the vslide-based technique can easily be applied to pairs of any element size (from 8-bit to 64-bit) or even to wider element groups (by setting multiple contigous mask bits to one to form a wider element with the maximal SEW). Another interesting factoid is that the mask and the vslide amount can even be built to work if the current SEW is not the width of the element: for example if you want to pair swap 32-bit elements while SEW=8-bit, you simply can use 0xf0 as the base mask pattern and 4 as the slide amount. This can save the use of a vsetvl.

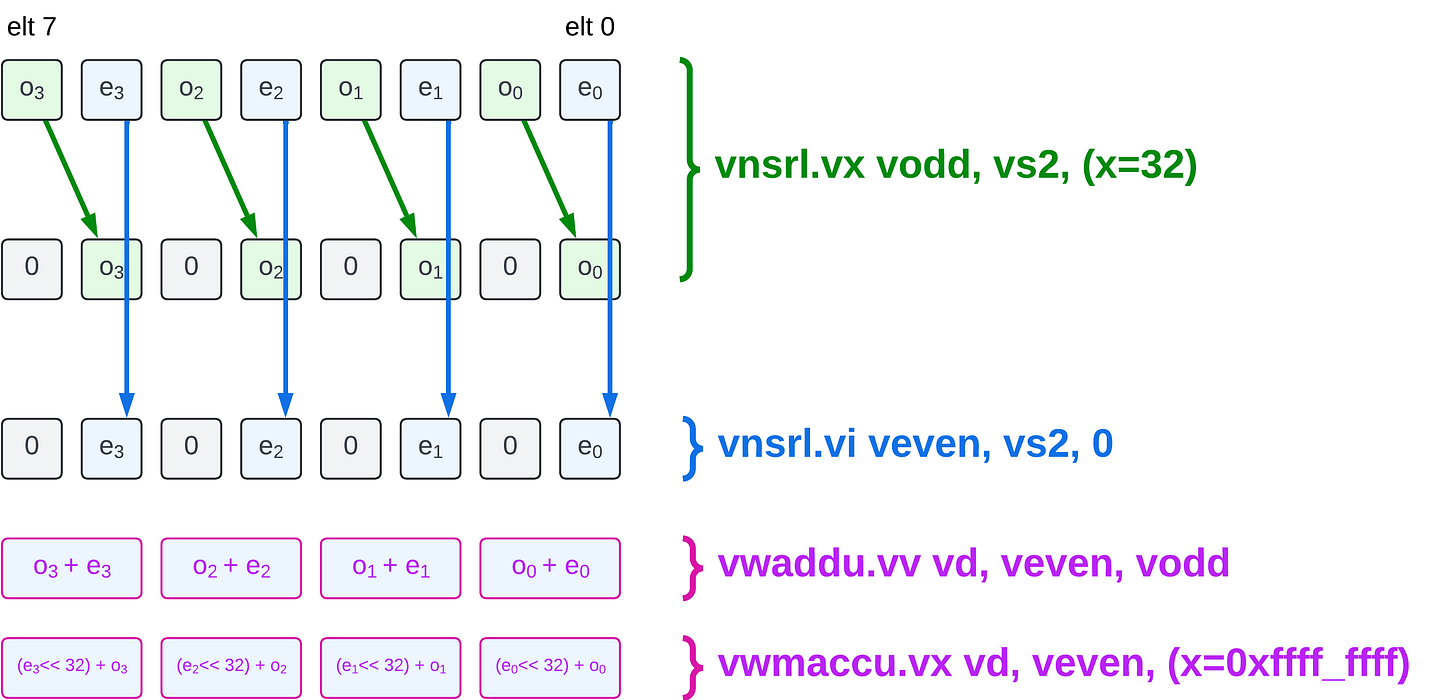
Using narrowing shifts and widening multiply-accumulate

The second technique we consider, leverages a well known method to zip (pair-combine) two vectors (this technique was described by Craig T. in this comment and listed by

camel-cdr

in his RVV Extension for Integer Workloads: An Informal Gap Analysis, a recommended read). It leverages RVV widening operations to perform the pair swap using only arithmetic instructions. This method interprets the 2x 32-bit pair (even, odd) as a 64-bit value equal to (odd « 32) + even. The method performs the swap by computing (even « 32) + odd. The idea is to compute the result as (2^32 -1) * even + even + odd. The initial (2^32 -1) * even can be expressed as a widening unsigned multiplication.

Note: This method only works to swap (even, odd) pairs, that is elements whose indices are 2k and 2k+1, where the even-indexed element appears with the lowest index. As is, it does not work for pairs 2k+1, 2k+2. Whereas the vslide-based method can be adapted for this case, by simply modifying the mask value, the widening-based approach would require extra slide instructions.

// Assuming vec_coeffs is a vector of vl 32-bit coefficiensts
// interpreted as unsigned values (vuint32_t)

// reinterpreting the vector as (vl/2) 64-bit pairs (2x 32-bit)
vuint64m1_t vec_coeffs_u64;
vec_coeffs_u64 = __riscv_vreinterpret_v_u32m1_u64m1(vec_coeffs);

vuint32m1_t vec_odd_coeffs, vec_even_coeffs;
// extracting odd and even coefficients, notice the use of a fractional
// LMUL (1/2, mf2) due to the use of a narrowing instruction with
// a LMUL=1 operand
vec_odd_coeffs  = __riscv_vnsrl_wx_u32mf2(vec_coeffs_u64, 32, vl / 2);
vec_even_coeffs = __riscv_vnsrl_wx_u32mf2(vec_coeffs_u64, 0, vl / 2);

// 2. vwmacc ()
// widening addition to get zext(o_i + e_i)
vec_coeffs_u64 = __riscv_vwaddu_vv_u64m1(vec_odd_coeffs, 
                                         vec_even_coeffs,
                                         vl / 2);
// Widening multiply-accumulate to add ((2^32 - 1) * e_i) to
// zext(o_i + e_i)
vec_coeffs_u64 = __riscv_vwmaccu_vx_u64m1(vec_coeffs_i64,
                                          -1, // 2^32 - 1
                                          vec_even_coeffs,
                                          vl / 2);

vuint32m1_t vec_swapped_coeffs;
// Finally casting the pair of coefficients as coefficients
vec_swapped_coeffs = __riscv_vreinterpret_v_u64m1_u32m1(vec_coeffs_u64);

Note: the use of RVV C-intrinsics mandates numerous calls to vreinterpret_v functions; those functions will not directly lead to the emission of actual instructions (although vset[i]vl[i] might be required when two successive instructions do not share the same LMUL/SEW configuration.

Benchmarking of element swap methods

We have integrated both approach in our NTT (fastest) implementation and run a few experimentations to compare them. Average latency results over 500 runs are reported below (a baseline result is reported, it replaces element swap by identity and is non-functional):

The full NTT latency is reported. For the same LMUL value, the vslide-based approach is always faster.

If we subtract the baseline latency, we get:

The conclusion is clear: the vslide-based technique using mask (and less operations) exhibits a much smaller latency than the widening arithmetic one. We have limited the comparison to large values of LMUL where both techniques were valid: vslide-based requires the use of a fractional LMUL after the narrowing shifts if the input LMUL is 1 and the widening-based technique cannot accomodate LMUL=8, since EMUL=2*LMUL for the widening operations. This also means that to apply on larger input vector register group the widening technique requires manual split while the vslide can be scaled to LMUL=8.

Conclusion

In this post we have presented, and compared, two straightforward techniques to perform pairwise swap using RISC-V Vector. Although, widening arithmetic can be efficient to zip two vectors, it appears to be less efficient than (un+)masked vslide when it comes to swapping pairs of element on the CanMV-K230. We will use this knowledge in a future post when we consider optimizing our NTT implementation Our goal is too get well below the 18’000 cycles implementation we presented with our intrinsic-based “fastest” implementation.

I have a few (lots) draft posts in the works, but I don’t think I will publish anymore this year ( 2024). Thank you to all the readers that have joined the “newsletter” this year or before, I hope you have found interesting information in the posts.

References:

• camel-cdr
  ‘s RVV Extension for Integer Workloads: An Informal Gap Analysis,